Login

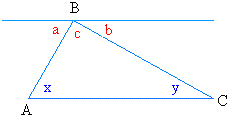
Can you explain me the angle sum property of a triangle ?

Consider a triangle PQR in which ∠1, ∠2 and ∠3 are the angles of Δ PQR (figure shown below). Angle sum property of a triangle says that sum of the three angles in a triangle is 180 degrees, i.e.,

 ∠1 + ∠2 + ∠3 = 1800.

https://s3mn.mnimgs.com/img/shared/userimages/mn_images/image/tri1.png

We will now see the proof of the above statement.

We use the properties related to parallel lines to prove this. For this, let us draw a line XPY parallel to QR through the opposite vertex P, as shown in the figure given below

https://s3mn.mnimgs.com/img/shared/userimages/mn_images/image/tri2.png

Now, XPY is a line.

Therefore, ∠4 + ∠1 + ∠5 = 1800 … (1)

But XPY || QR and PQ, PR are transversals.

So, ∠4 = ∠2 and ∠5 = ∠3 (Pairs of alternate angles)

Substituting ∠4 and ∠5 in (1), we get

∠2 + ∠1 + ∠3 = 1800

That is, ∠1 + ∠2 + ∠3 = 1800

  • 41
View Full Answer

Angle Sum Property Of A Triangle States That The Sum Of All Angles Of A Triangle Is 180 degree

i.e. angle 1+angle2+angle3=180degree

  • -2

 Angle Sum Theorem of a Triangle

The sum of the measures of the interior angles of a triangle is 180.

  • 3
Angle-sum-theorem-image

 

Since angle a, angle b, and angle c make a straight line,

angle a + angle b + angle c = 180 degrees

Since alternate interior angles are equal, angle a = angle x and angle b = angle y

Therefore, angle x + angle y + angle c = 180 degrees 

  • 4

Angle Sum of a Triangle

With the use of the Parallel Postulate, the following theorem can be proven.

Theorem 25: The sum of the interior angles of any triangle is 180°.

m ∠ A + m ∠ B + m ∠ C = 180°.

Example 1: If m ∠ A = 40° and m ∠ B = 60°, find m ∠ C.



 

  • 10

sum of all the angles of a triange is known as angle sum property

the sum of all angles in a triangle is 180 degree

  • -7
What are you looking for?