prove that in a triangle the line segment joining the mid points of any to sides is parallel to the third side.

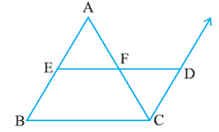
Given : E and F are the midpoints of AB and AC respectively.  

               CD II AB

in triangles AEF and CDF,

angle AFE = angle CFD      (vertically opposite angles)

AF = CF                                   (F is the midpoint of AC)

angle EAF = angle FCD        (alternate interior angles)

therefore, triangles AEF and CDF are congruent by ASA  congruence.

therefore, EF = DF (CPCT)

AE = EB = CD     (CPCT)

In quadrilateral BCDE, 

EB = CD  and CD II BA

therefore, BCDE is a parallelogram            (since a quadrilateral is a parallelogram if a pair of opposite sides are equal

                                                                               and parallel)

therefore, EF II BC

hence, Proved.

hope it helped   :)